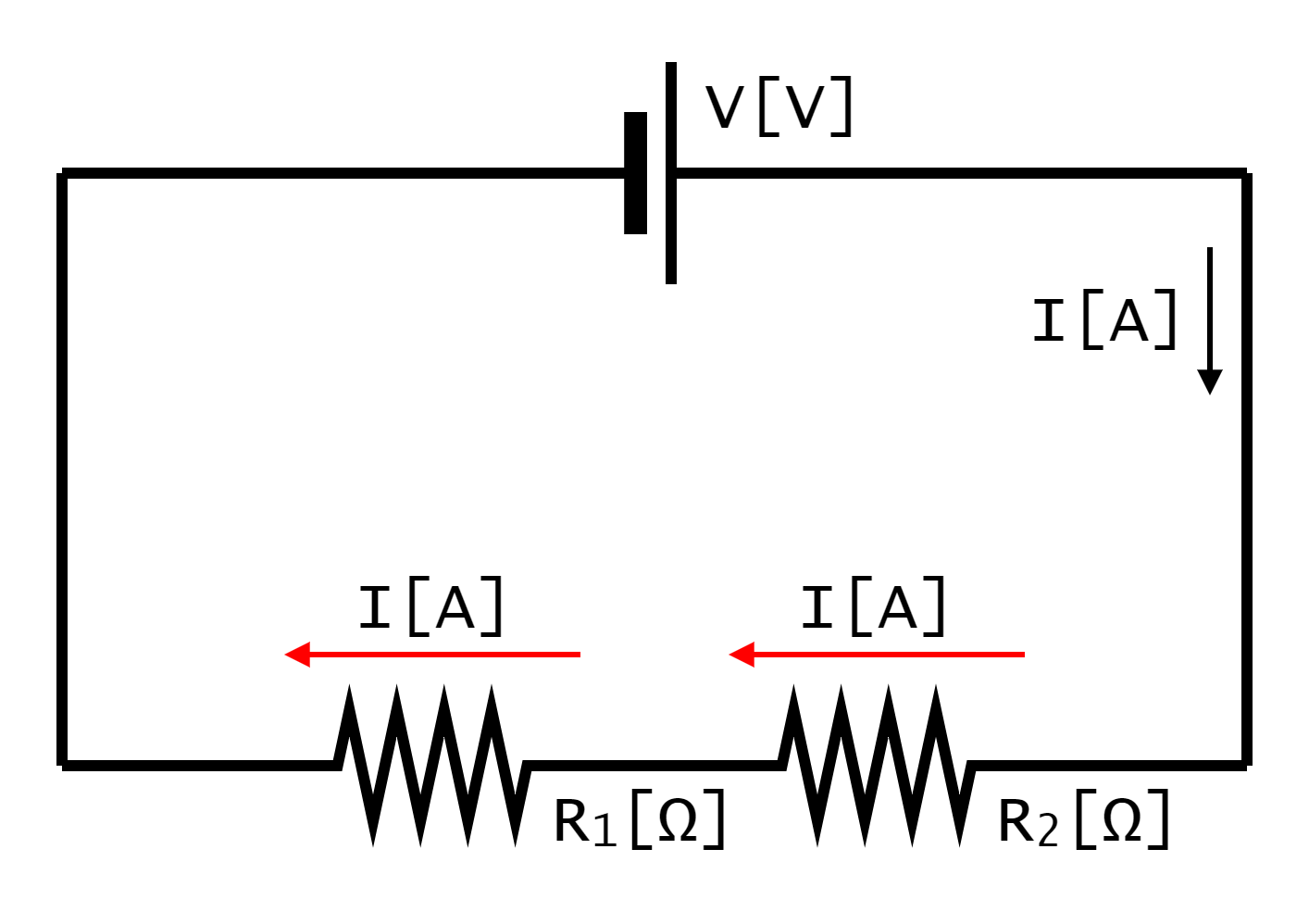
分流
抵抗器を並列接続した電気回路(電子回路)を使って、分流を解説します。
1-5-1.抵抗器を流れる電流
1-5-2.分流とは
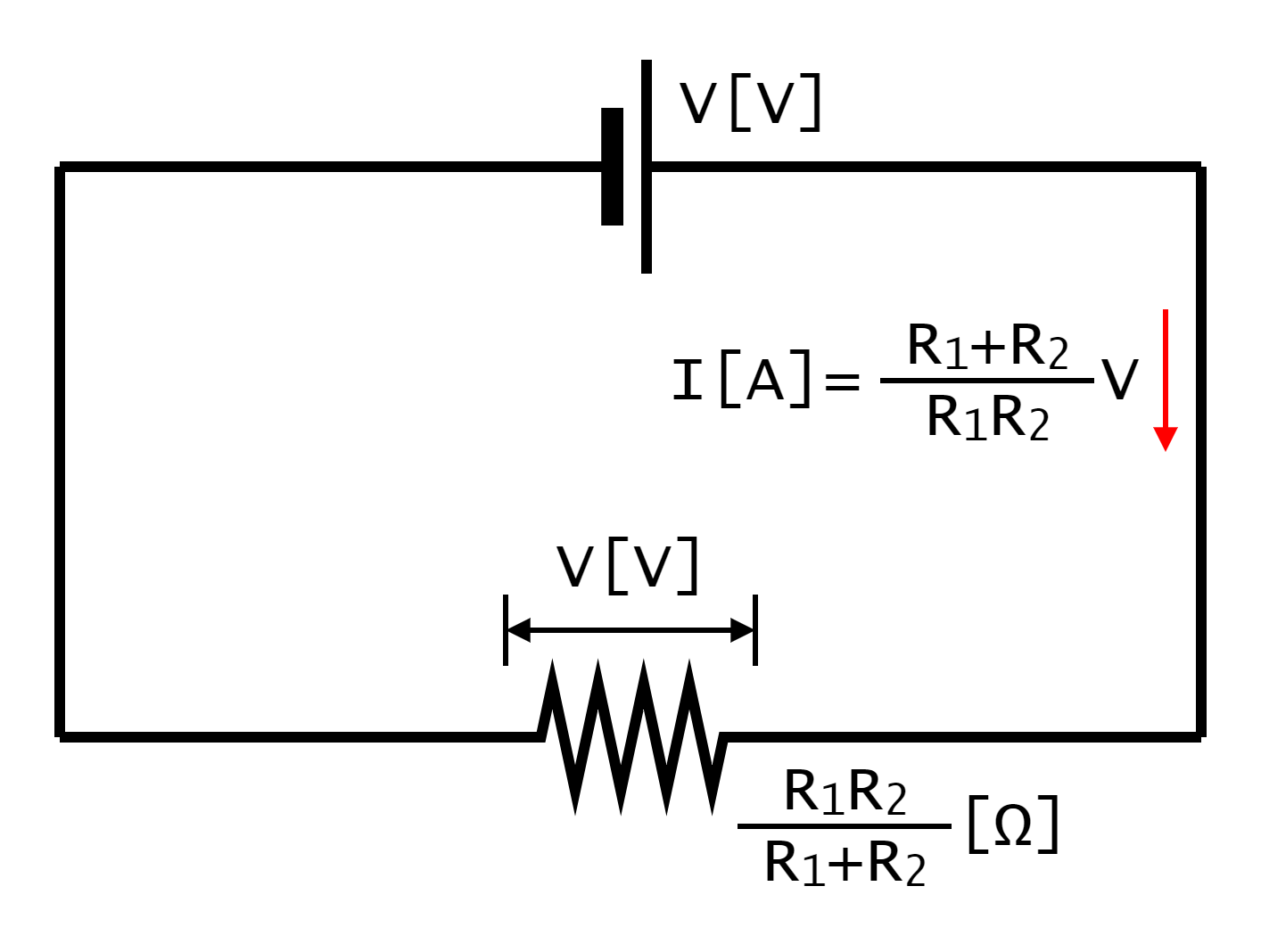
まず、電流I[A]について考えます。電流I[A]を求めるために、二つの抵抗R1[Ω]・R2[Ω]の合成抵抗を考えます。二つの抵抗器は並列接続なので、合成抵抗は「逆数の和の逆数」で求められ、合成抵抗は(R1×R2)÷(R1+R2)[Ω]となります。合成抵抗を一つの抵抗器を見なすと、その抵抗器に加わる電圧はV[V]となります。電流I[A]は、オームの法則より電圧÷抵抗で求められるので、この電気回路(電子回路)の電流I[A]は図1-5-2-1に示したようになります。
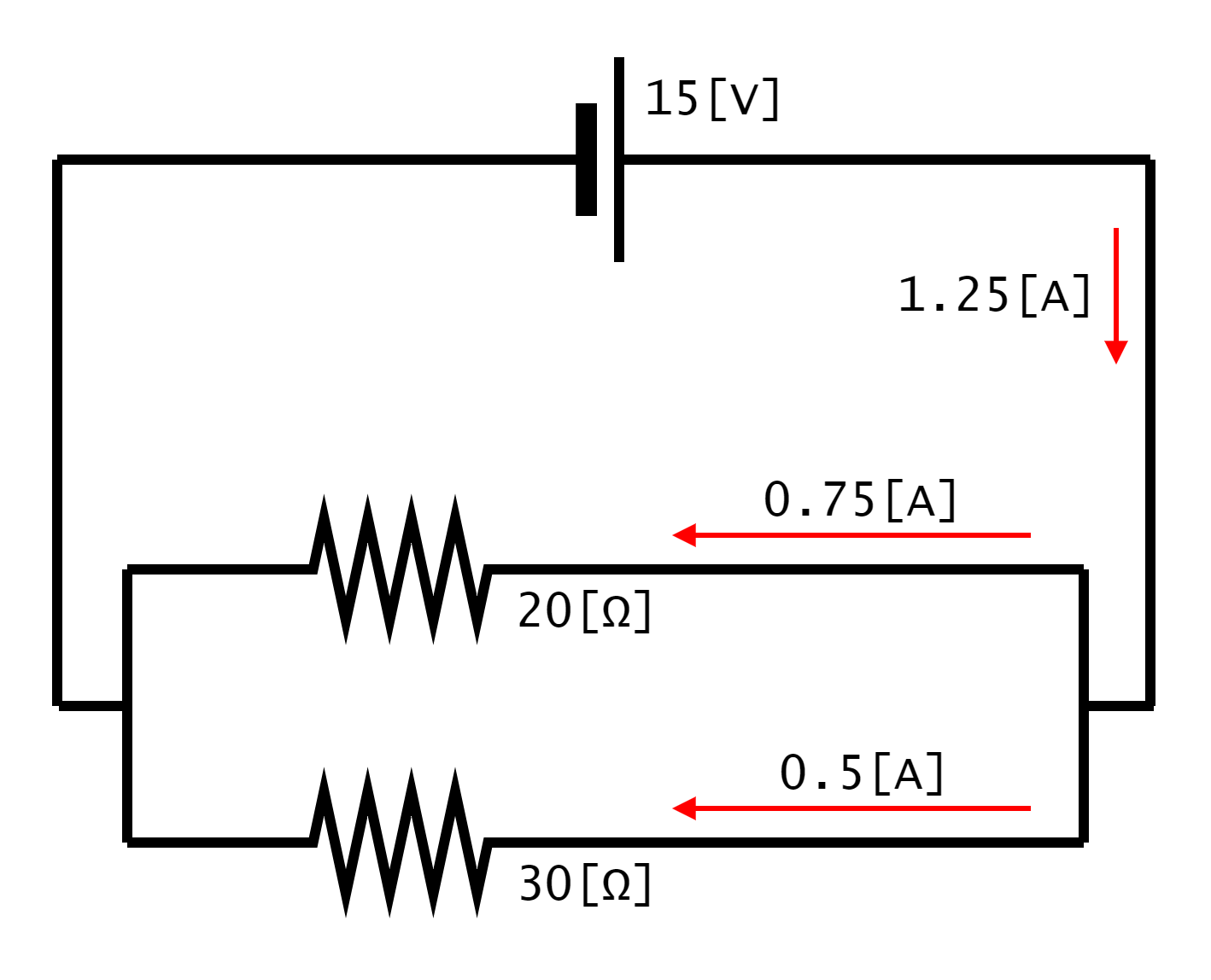
ここで、電流I[A]と各抵抗器に流れる電流I1[A]・I2[A]の関係について考えます。図1-5-2-2を見ると、電流I[A]と、各抵抗器に流れる電流I1[A]・I2[A]の和が等しいことがわかります。つまり、電流I[A]が、各抵抗器に分割されているということになります。
このように、並列接続において、電流が分割されることを「分流」といいます。
では、分割された電流の比はどのようになっているのでしょうか。まず、抵抗R1[Ω]に流れる電流I1[A]を考えます。I1[A]の全体に対する割合は、I1÷Iで求められます。計算すると、R2÷(R1+R2)となります。同様に、抵抗R2[Ω]に流れる電流の割合は、R1÷(R1+R2)となります。抵抗R1[Ω]・R2[Ω]によって分割される電流の比はR2:R1であるといえます。
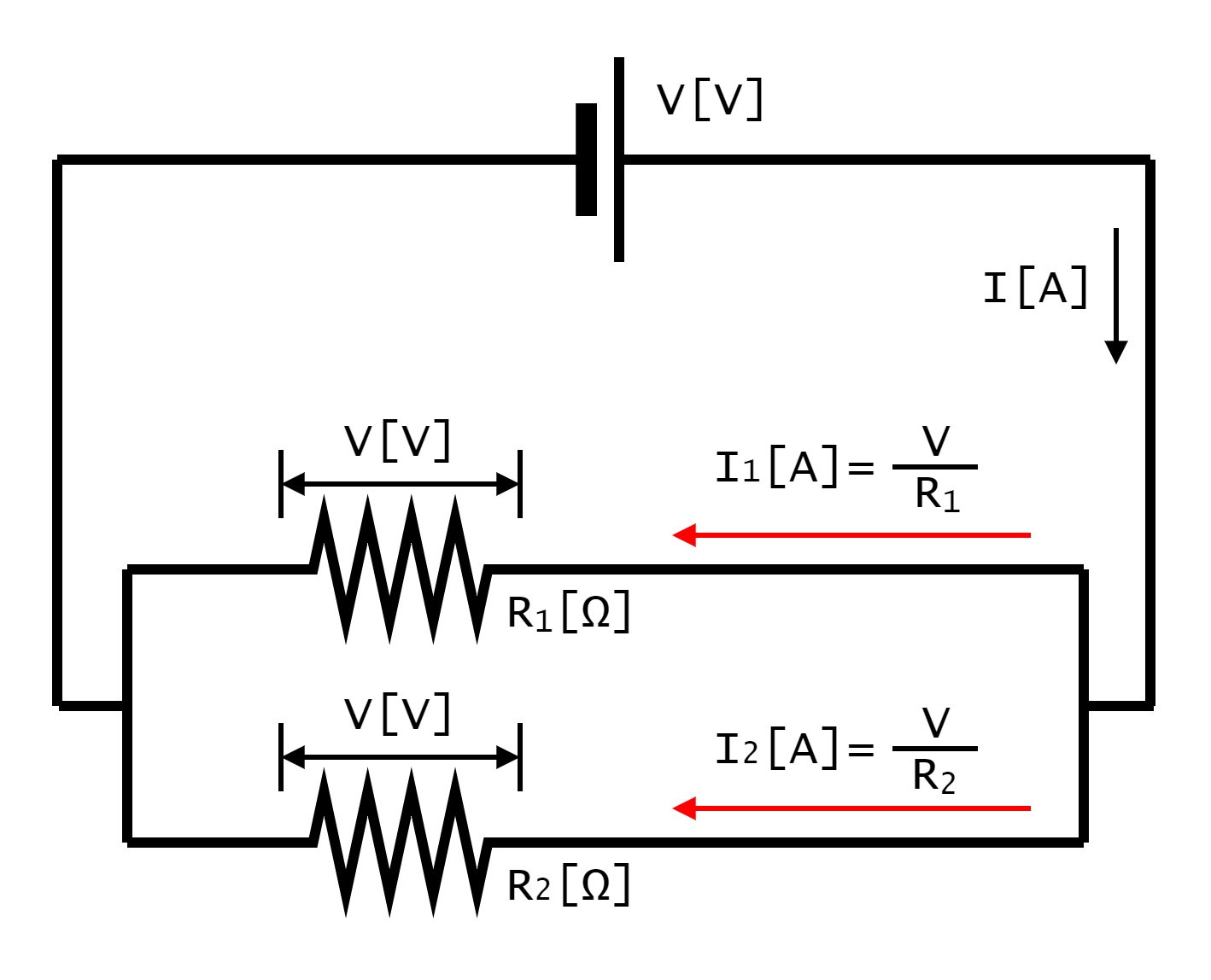
![図1-5-2-2.電流I[A]と各抵抗器に流れる電流I1[A]・I2[A]の関係](/make-electronics/images/chapter-1/current-division-03.png)