分圧
抵抗器を直列接続した電気回路(電子回路)を使って、分圧を解説します。
1-4-1.抵抗器に加わる電圧
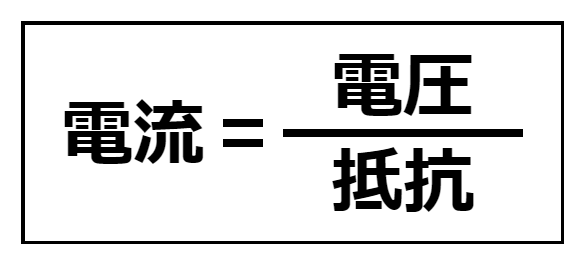
1-1.電気の流れを考える【オームの法則】では、基本かつ最も重要な関係式の一つとして、オームの法則を解説しました。図1-4-1-1は、オームの法則を表す関係式です。「抵抗」は抵抗器の「電気の流れを妨げる力」、「電流」は電気回路(電子回路)を「流れる電気の量」です。では、この関係式の「電圧」とはどの部分なのでしょうか。
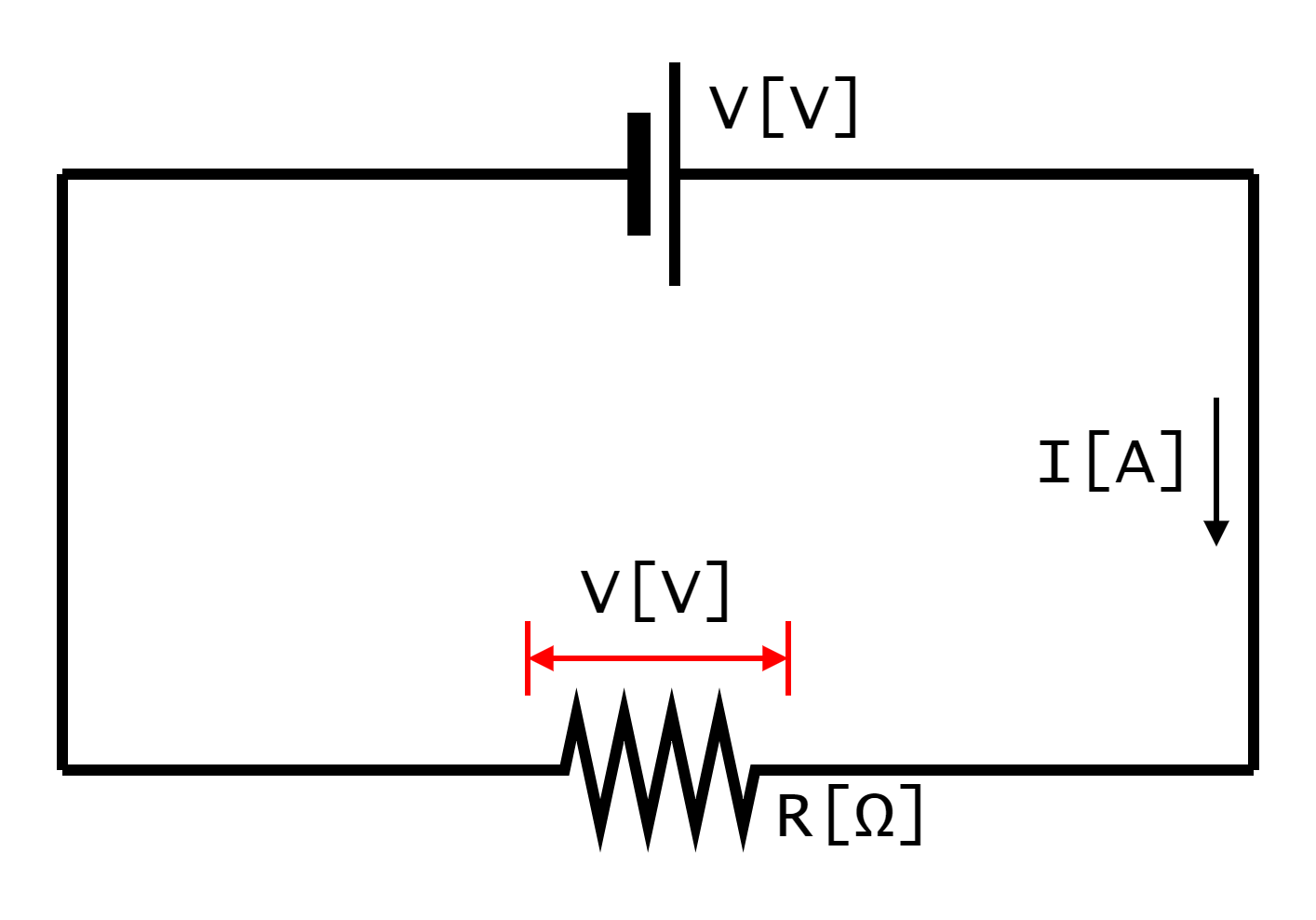
図1-4-1-2は、一つの直流電源と一つの抵抗器からなる電気回路(電子回路)です。直流電源の電圧をV[V(ボルト)]、電流をI[A(アンペア)]、抵抗をR[Ω(オーム)]とします。
「電圧」とは、直流電源が「電気を押し出す力」のことですが、実はこの「電気を押し出す力」が、抵抗器にも作用しています。これを抵抗器に電圧が加わる、または印加(いんか)されるといいます。赤い矢印で示した部分です。
この電気回路(電子回路)のように、直流電源に対して、抵抗器が一つの場合、抵抗器に加わる電圧は、直流電源の電圧に等しくなります。
1-4-2.分圧とは
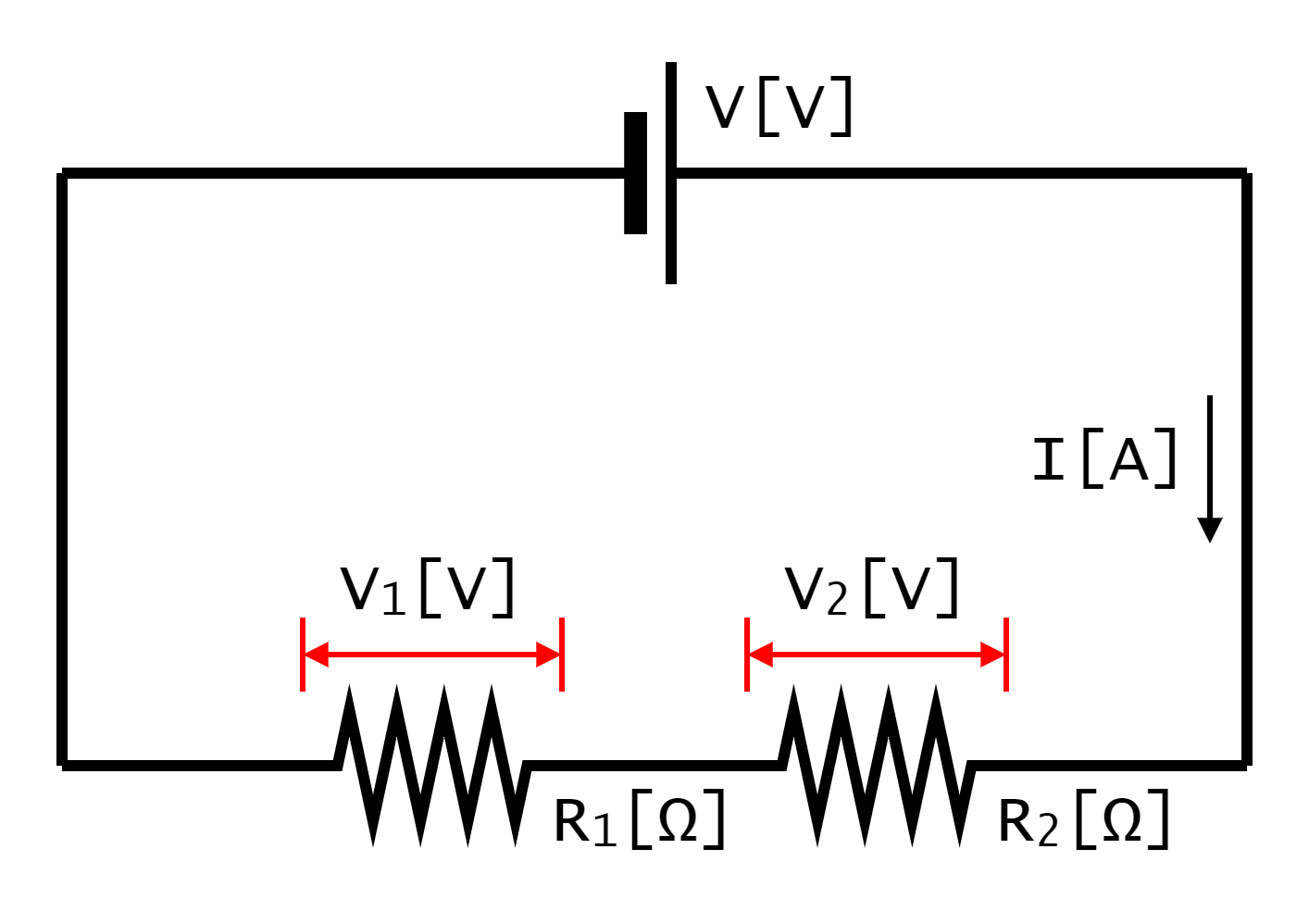
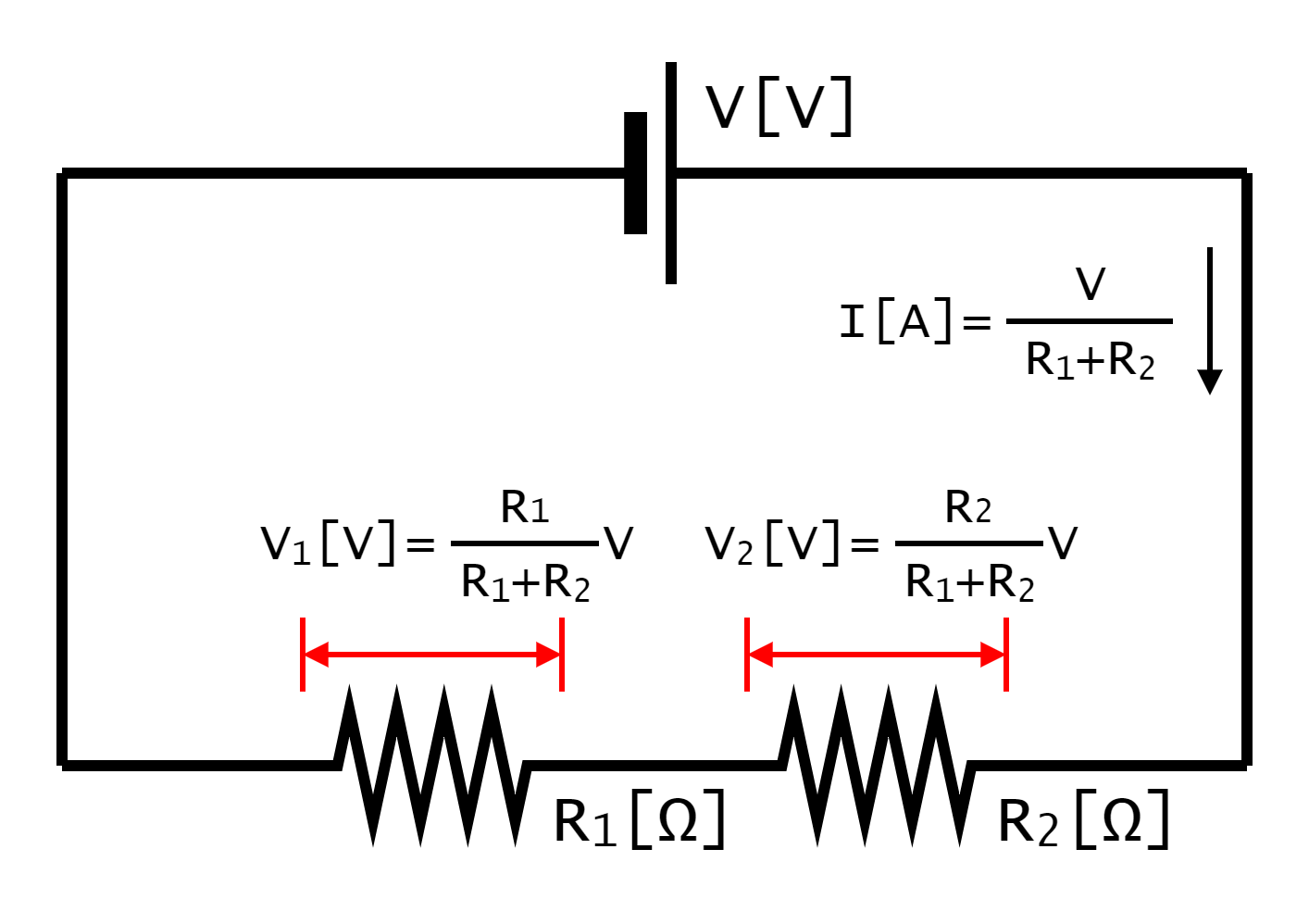
では、複数の抵抗器がある場合はどうなるのでしょうか。図1-4-2-1は、二つの抵抗器を直列接続した電気回路(電子回路)です。この時の抵抗R1[Ω]・R2[Ω]にかかる電圧を考えてみます。
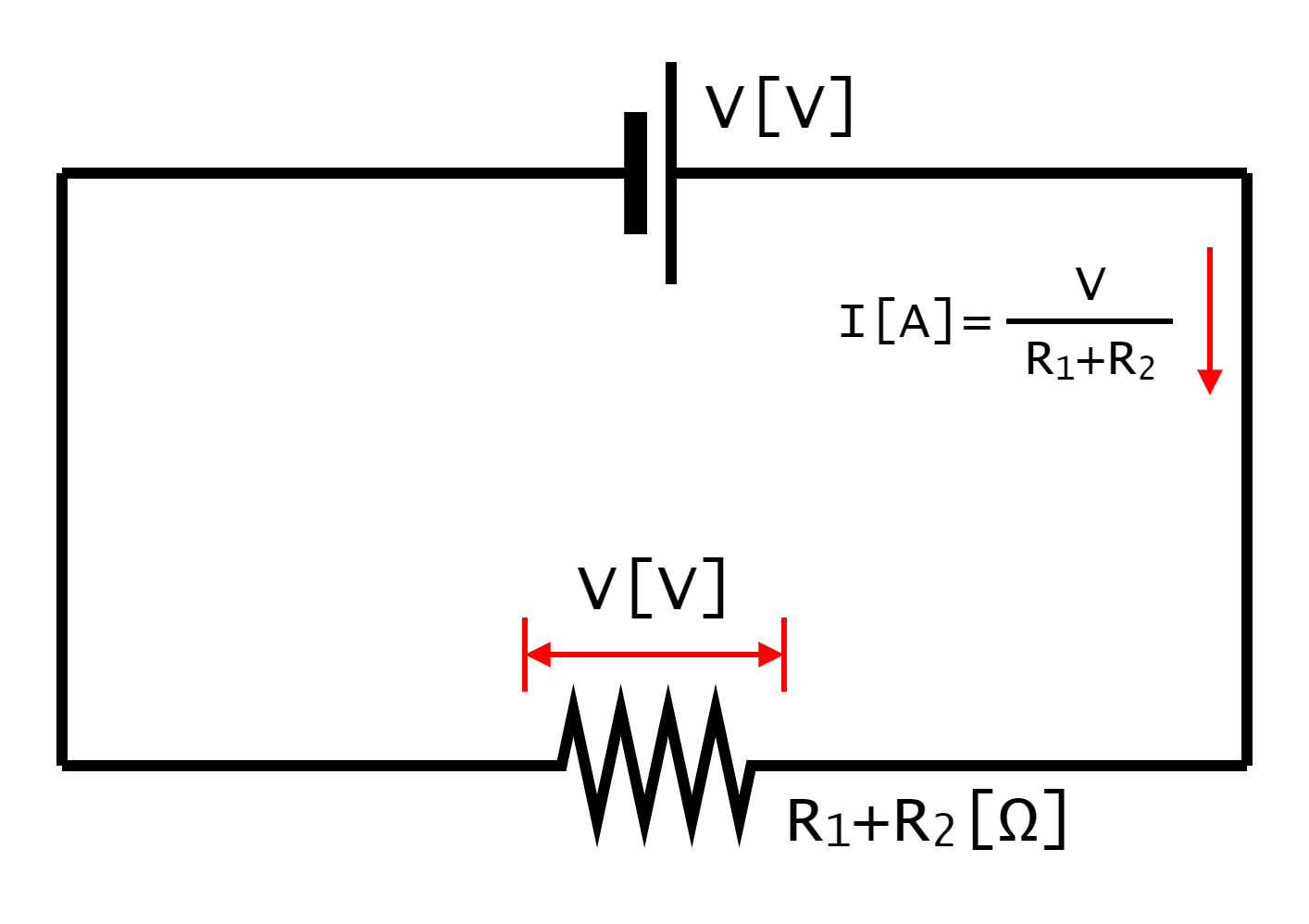
まず、電流I[A]を求めるために、二つの抵抗R1[Ω]・R2[Ω]の合成抵抗を考えます。二つの抵抗器は直列接続なので、合成抵抗はそのまま加算することで求められ、合成抵抗はR1+R2[Ω]となります。合成抵抗を一つの抵抗器を見なすと、その抵抗器に加わる電圧はV[V]となります。電流I[A]は、オームの法則より電圧÷抵抗で求められるので、この電気回路(電子回路)の電流I[A]は図1-4-2-2に示したようになります。
電流I[A]は、直列接続の場合、抵抗R1[Ω]・R2[Ω]に等しく流れます。抵抗R1[Ω]・R2[Ω]にかかる電圧V1[V]・V2[V]は、オームの法則より電流×抵抗で求められるので、電圧V1[V]・V2[V]は図1-4-2-3に示したようになります。
抵抗R1[Ω]・R2[Ω]にかかる電圧V1[V]・V2[V]が求められました。難しそうに見える式ですが、よく見ると直流電源の電圧V[V]に対して、各抵抗R1[Ω]・R2[Ω]の比(R1:R2)で分割されていることがわかります。R1[Ω]÷(R1[Ω]+R2[Ω])、R2[Ω]÷(R1[Ω]+R2[Ω])の部分をV[V]の係数と考えるとわかりやすくなります。
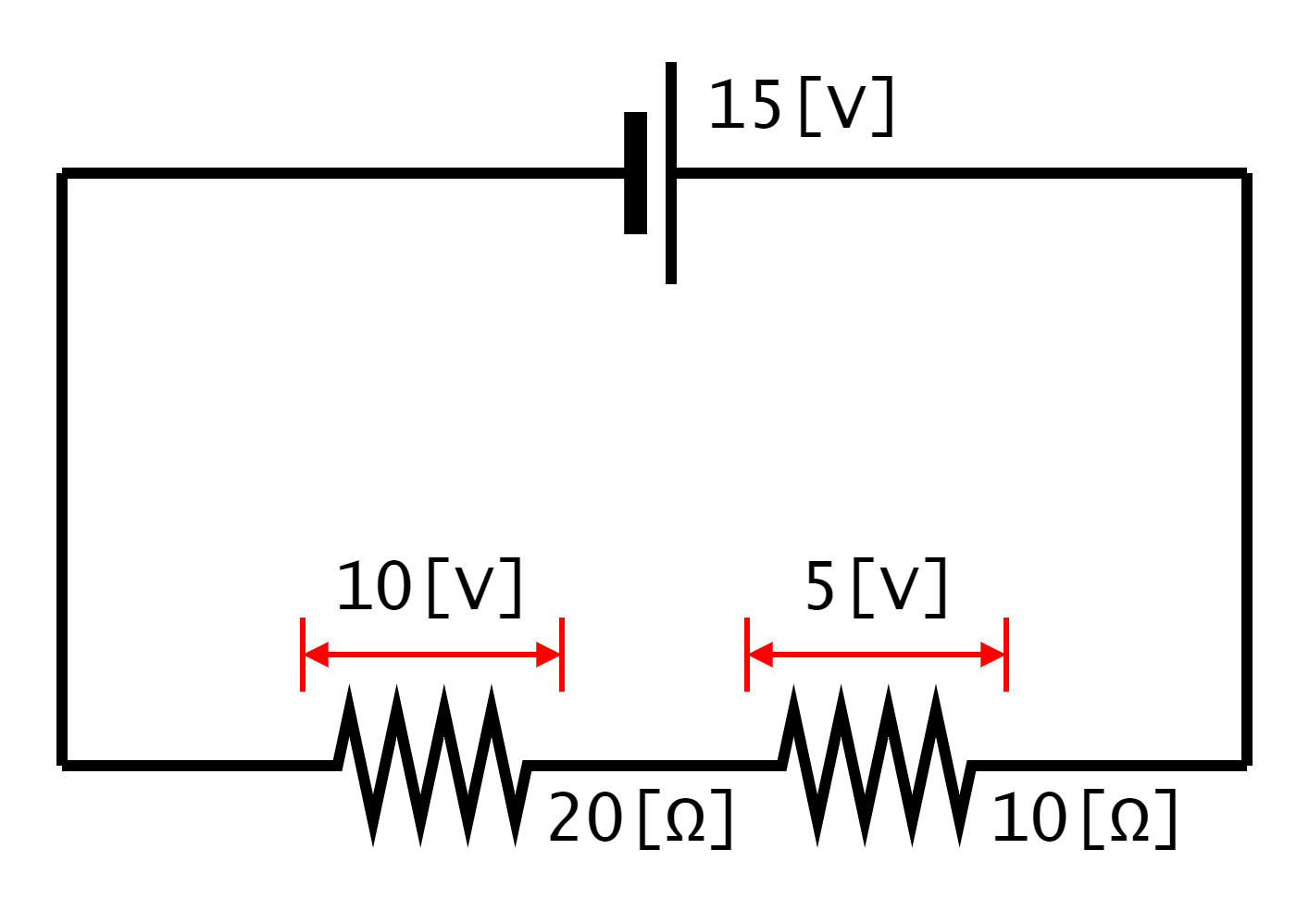
このように直列接続において、電圧が分割されることを「分圧」といい、抵抗器の場合、各抵抗の比によって分圧されます。また、分圧された電圧をすべて加えると、直流電源の電圧に等しくなります。