合成抵抗
直列接続または並列接続された抵抗器における合成抵抗の求め方を解説します。
1-3-1.合成抵抗とは
1-2.直列接続と並列接続では、二つ以上の抵抗器を接続する方法として、直列接続と並列接続を解説しました。二つ以上の抵抗器を接続した時、あたかも一つの抵抗器と等価と考え、その抵抗を求めることができます。また、求めた抵抗を「合成抵抗」といいます。
1-3-2.直列接続の合成抵抗
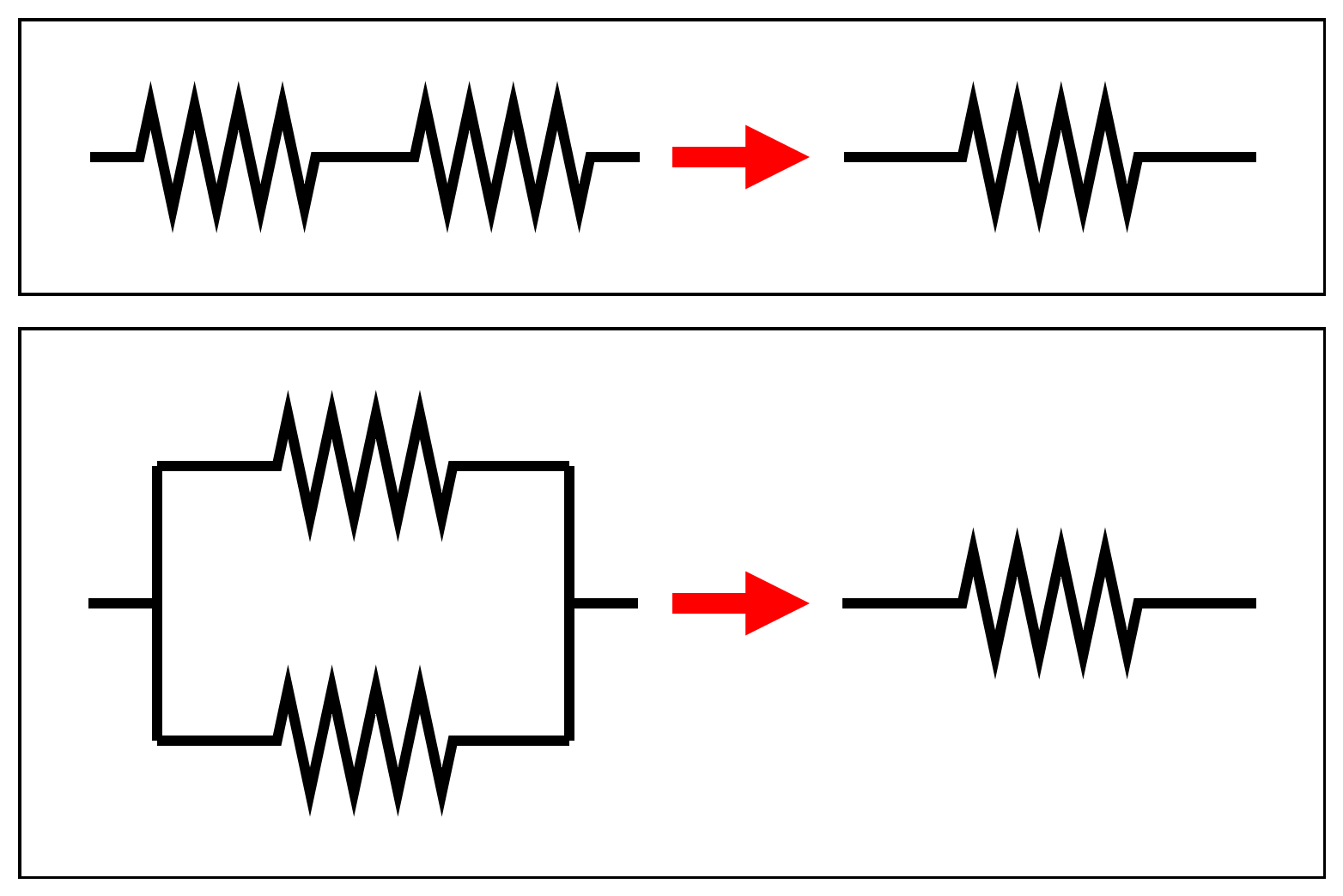
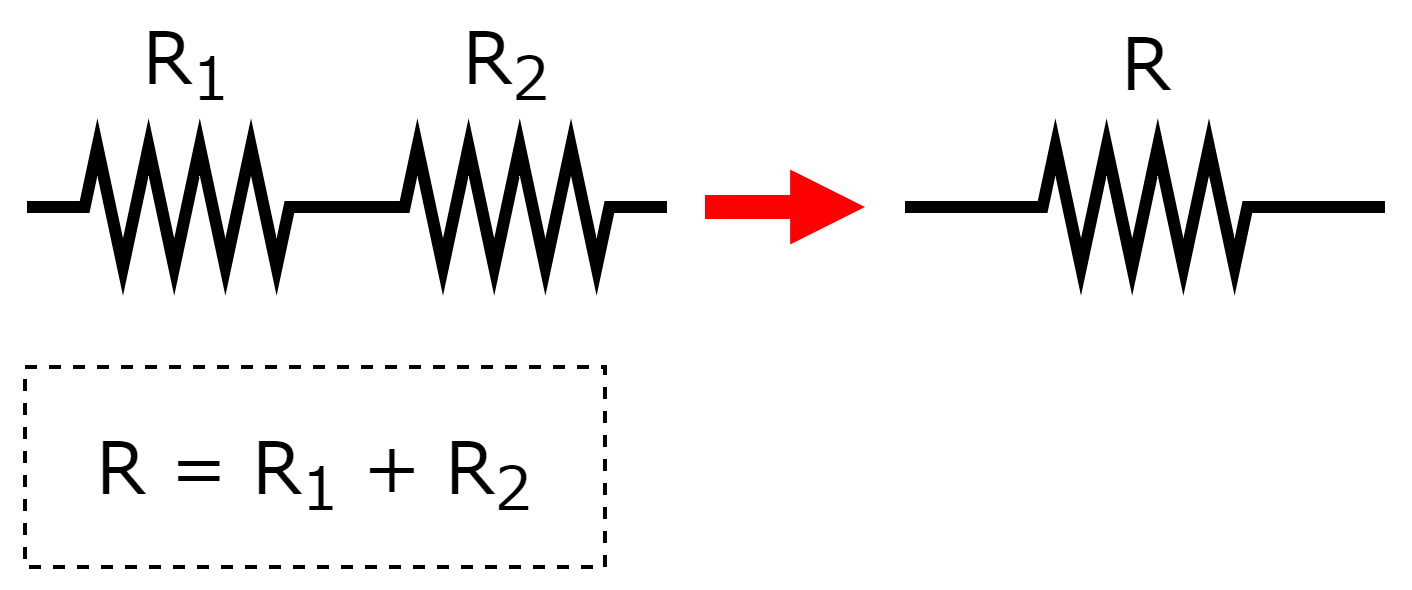
直列接続の合成抵抗(R[Ω])を求めるには、各抵抗器の抵抗(R1[Ω]・R2[Ω])を「そのまま加算」します。
直列接続で求められた合成抵抗は、各抵抗器の抵抗いずれよりも大きな値となります。
R>R1 かつ R>R2
抵抗は「電気の流れを妨げる力」なので、大きくなるということは電気が流れにくくなるということです。直列接続は、より大きな抵抗を作り出すことができる接続方法といえます。
同じ抵抗の抵抗器を二つ直列接続した場合、抵抗は二倍になります。例えば、150Ωの抵抗器を二つ直列接続した場合、その合成抵抗は150Ω+150Ω=300Ωとなります。
また、三つ以上直列接続した場合も、同様に加算することで合成抵抗が求められます。例えば、150Ωの抵抗器を三つ直列接続した場合、その合成抵抗は150Ω+150Ω+150Ω=450Ωとなります。
1-3-3.並列接続の合成抵抗
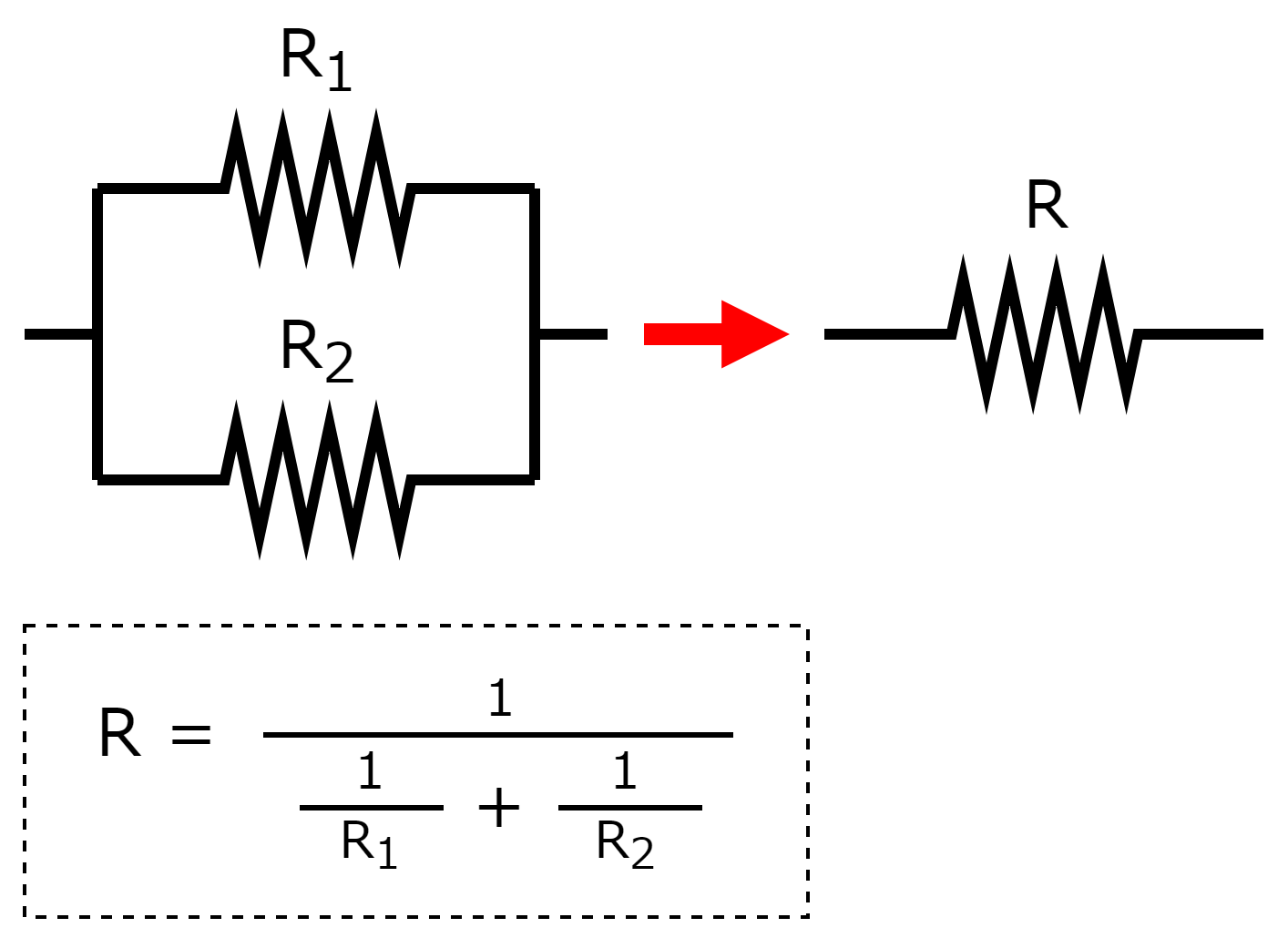
並列接続の合成抵抗(R[Ω])は、各抵抗器の抵抗(R1[Ω]・R2[Ω])において「逆数の和の逆数」で求められます。逆数とは、分母と分子を入れ替えたもので、抵抗R1の逆数は、1/R1(R1分の1)となります。
抵抗の逆数とはどういったものなのでしょうか。抵抗は「電気の流れを妨げる力」でした。その力の逆ということは「電気の流れやすさ」を示す値といえます。この「電気の流れやすさ」をコンダクタンスといい、S(ジーメンス)という単位で表されます。
つまり、計算式の前半部分「逆数の和」とは、各抵抗器における「電気の流れやすさ」の和ということになります。これが、並列接続されたすべての抵抗器を一つとして考えた「電気の流れやすさ」に等価となります。続いて、その「電気の流れやすさ」の和を逆数にすることで、「電気の流れを妨げる力」となり、全体の合成抵抗が求められます。これが「逆数の和の逆数」の意味です。
並列接続で求められた合成抵抗は、各抵抗器の抵抗いずれよりも小さな値となります。
R<R1 かつ R<R2
抵抗は「電気の流れを妨げる力」なので、小さくなるということは電気が流れやすくなるということです。並列接続は、より小さな抵抗を作り出すことができる接続方法といえます。
同じ抵抗の抵抗器を二つ並列接続した場合、抵抗は半分になります。例えば、150Ωの抵抗器を二つ並列接続した場合、その合成抵抗は1÷(1÷150Ω+1÷150Ω)=75Ωとなります。
また、三つ以上並列接続した場合も、同様に「逆数の和の逆数」することで合成抵抗が求められます。例えば、150Ωの抵抗器を三つ並列接続した場合、その合成抵抗は1÷(1÷150Ω+1÷150Ω+1÷150Ω)=50Ωとなります。