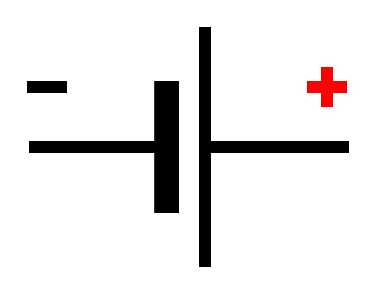電気の流れを考える【オームの法則】
電気の流れに注目して、電圧・電流・抵抗の関係を考えます。基本かつ最も重要な関係式の一つである「オームの法則」を解説します。
1-1-1.閉じた水路を考える
電気の流れを説明する時、よく、流れる水に例えられます。ここでは、ポンプから押し出された水が、水車を回す例を考えてみます。説明に使うのは、図1-1-1-1です。
まず最初に、使用するマークについて紹介します。図1-1-1-2のマークは、ポンプです。ポンプは、水の流れを作ります。マークの中に描かれた矢印は、水を押し出す方向と、力の大きさを表しています。この図では、右側へ水を押し出しています。
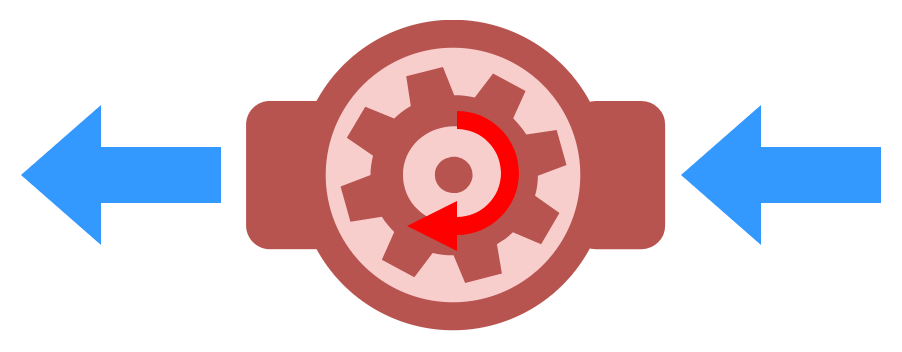
図1-1-1-3のマークは、水車です。水車は、流れる水によって回ります。マークの中に描かれた水車は、その羽の大きさを表しています。この図では、右側から流れ込む水によって、水車が回っています。
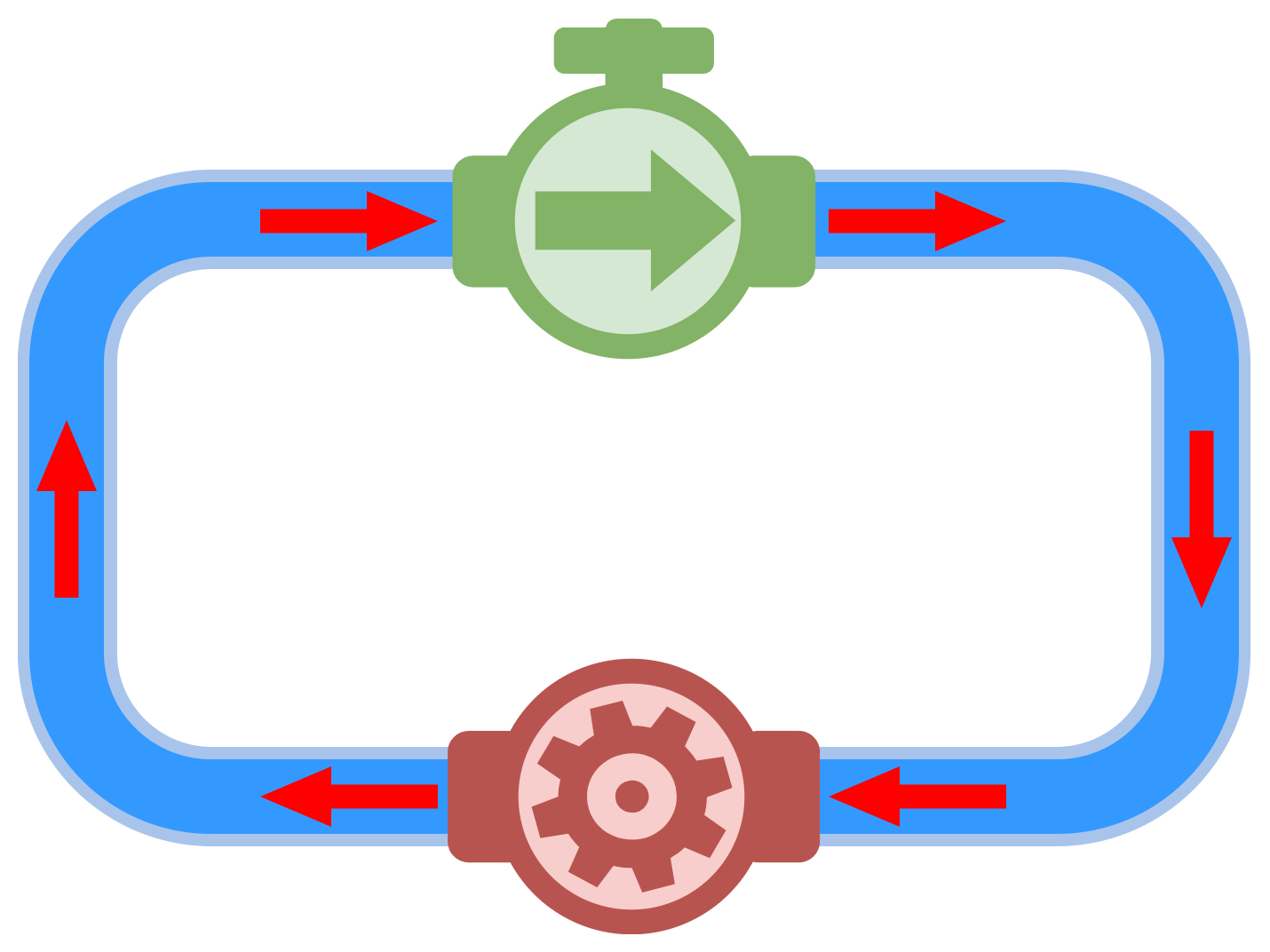
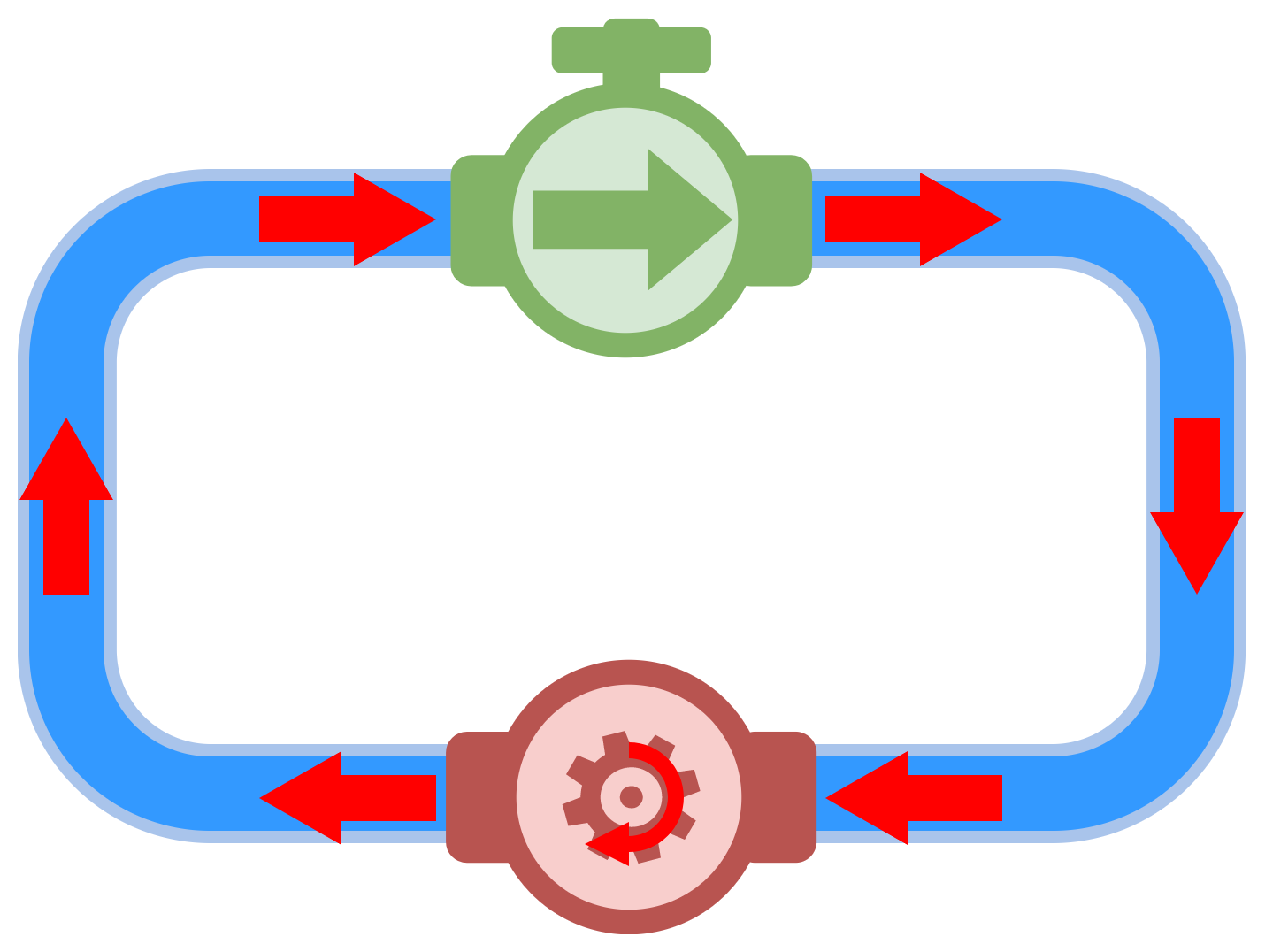
図1-1-1-4は、ポンプから押し出された水が、水車へ伝わるように、水の流れるパイプで接続したものです。図中の赤い矢印が、水の流れる方向と大きさ(流れる量)を表しています。ポンプから押し出された水は、水車を通って、再びポンプに戻ってくる「閉じた水路」です。この図を使って、水の流れるようすを観察します。
1-1-2.ポンプに注目する
まず、ポンプに注目して「水の流れ」を見てみましょう。赤い矢印は、ポンプの力によって水が押し出され、パイプを通って水車に伝わり、再びパイプを通ってポンプに戻るようすを表しています。この赤い矢印が「水の流れ」であり「水の流れる量」には、ポンプの力による「水を押し出す力」が関係しているといえます。
では、ポンプの力が変化すると「水の流れる量」はどうなるでしょうか。
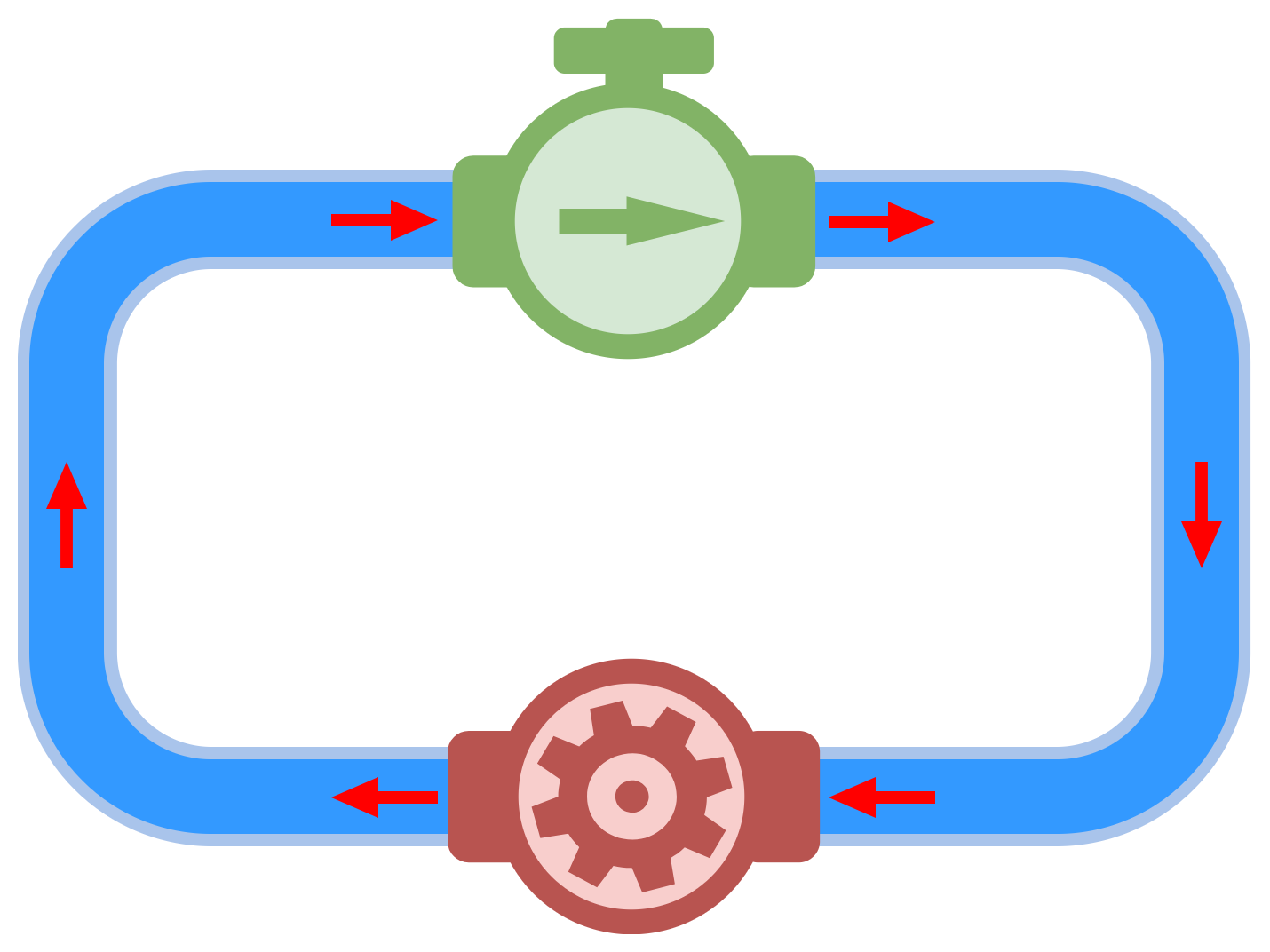
ポンプの力が弱まると・・・(緑色の矢印が小さくなると・・・)
「水の流れる量」が少なくなりました。(赤色の矢印も小さくなりました。)
これは、ポンプの力が弱まることで「水を押し出す力」が小さくなり、その結果「水の流れる量」が少なくなったと考えられます。
1-1-3.水車に注目する
次に、水車に注目して「水の流れ」を見てみましょう。まず、水車の動きを考えます。水車は、流れる水が羽に当たり、その力によって羽が送り出されることで、車軸を中心にして回転します。流れる水が羽に当たるということは、そこで「水の流れ」が弱まるということです。つまり「水の流れ」には、水車による「水の流れを妨げる力」が働いているということになります。
では、水車の大きさが変化すると「水の流れる量」はどうなるでしょうか。
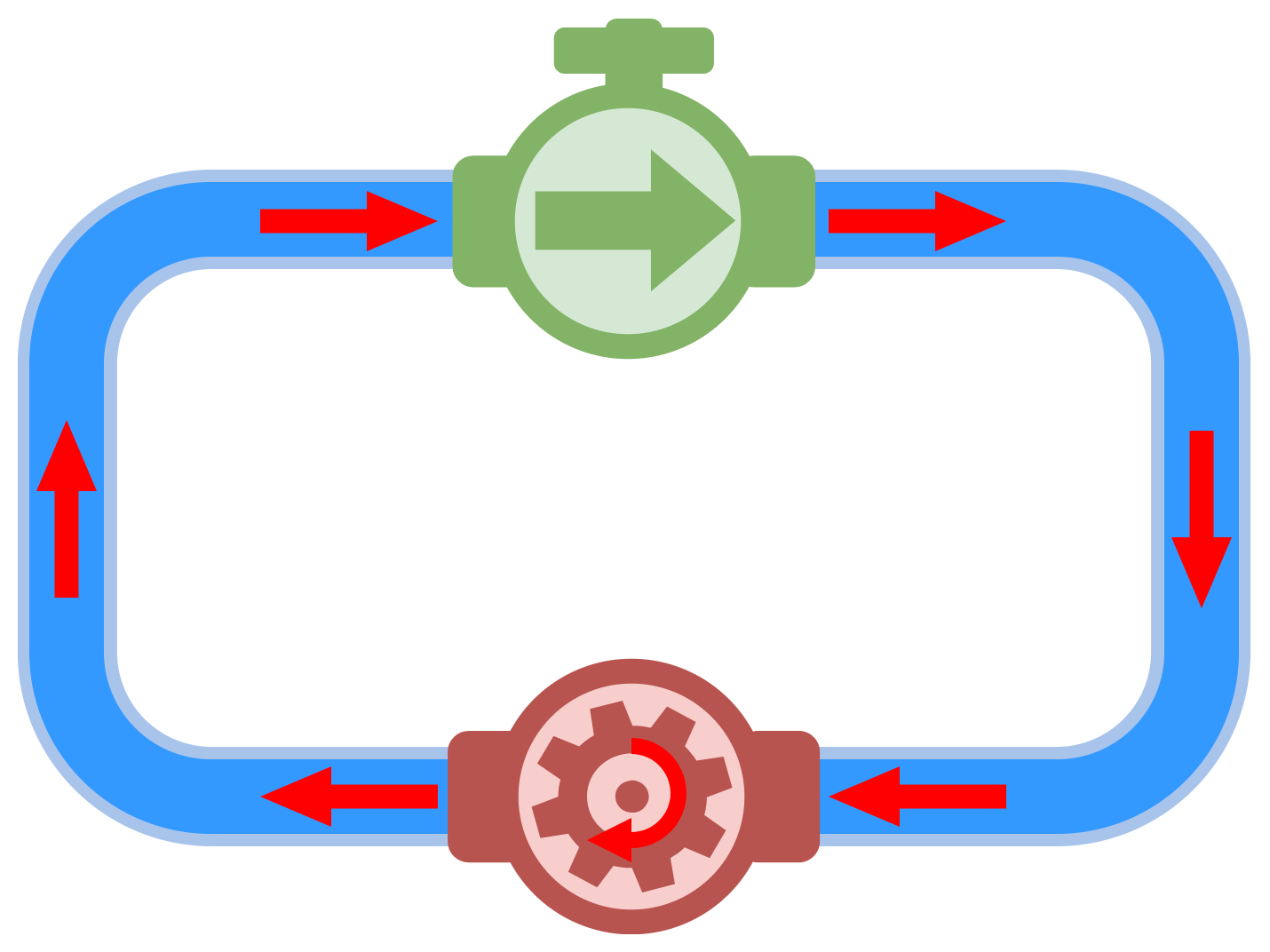
水車が小さくなると・・・(水車のマークが小さくなると・・・)
「水の流れる量」が多くなりました。(赤色の矢印は大きくなりました。)
これは、水車が小さくなることで「水の流れを妨げる力」が弱くなり、その結果「水の流れる量」が多くなったと考えられます。
1-1-4.閉じた水路からわかること
「閉じた水路」から、次のようなことがわかりました。
- 「水を押し出す力」が小さく(大きく)なる → 「水の流れる量」が少なく(多く)なる
- 「水の流れを妨げる力」が小さく(大きく)なる → 「水の流れる量」が多く(少なく)なる
どうやら「閉じた水路」では、「水の流れる量」に「水を押し出す力」と「水の流れを妨げる力」の二つが深く関係しているようです。
1-1-5.あらためて電気の流れを考える
では、あらためて電気の流れを考えてみましょう。水の流れと、電気の流れはとてもよく似ています。図1-1-5-1を見てください。これは「閉じた水路」を、電気の世界に置き換えたものです。「閉じた水路」に相当するものを「電気回路」、または対象を電子工学(弱電)に限って「電子回路」といいます。
「ポンプ」に相当するものを「直流電源」といい、代表的なものに乾電池があります。ポンプが水を押し出すように、直流電源は一定の力で電気を押し出します。この「電気を押し出す力」を「電圧」といい、V(ボルト)という単位で表されます。乾電池の電圧は、種類によって1.5V(円筒型単電池)・9V(平形6層電池)などがあります。
図1-1-5-2は、直流電源を表す記号です。縦の長い線側をプラス極(+)、短い線側をマイナス極(-)といい、プラス極から押し出された電気は、接続された電気回路(電子回路)を通ってマイナス極へ流れます。
「水車」に相当するものを「抵抗器」といいます。水車が水の流れを妨げるように、抵抗器は電気の流れを妨げます。この「電気の流れを妨げる力」を「抵抗」といい、Ω(オーム)という単位で表されます。
図1-1-5-3は、抵抗器を表す記号です。極性はありません。
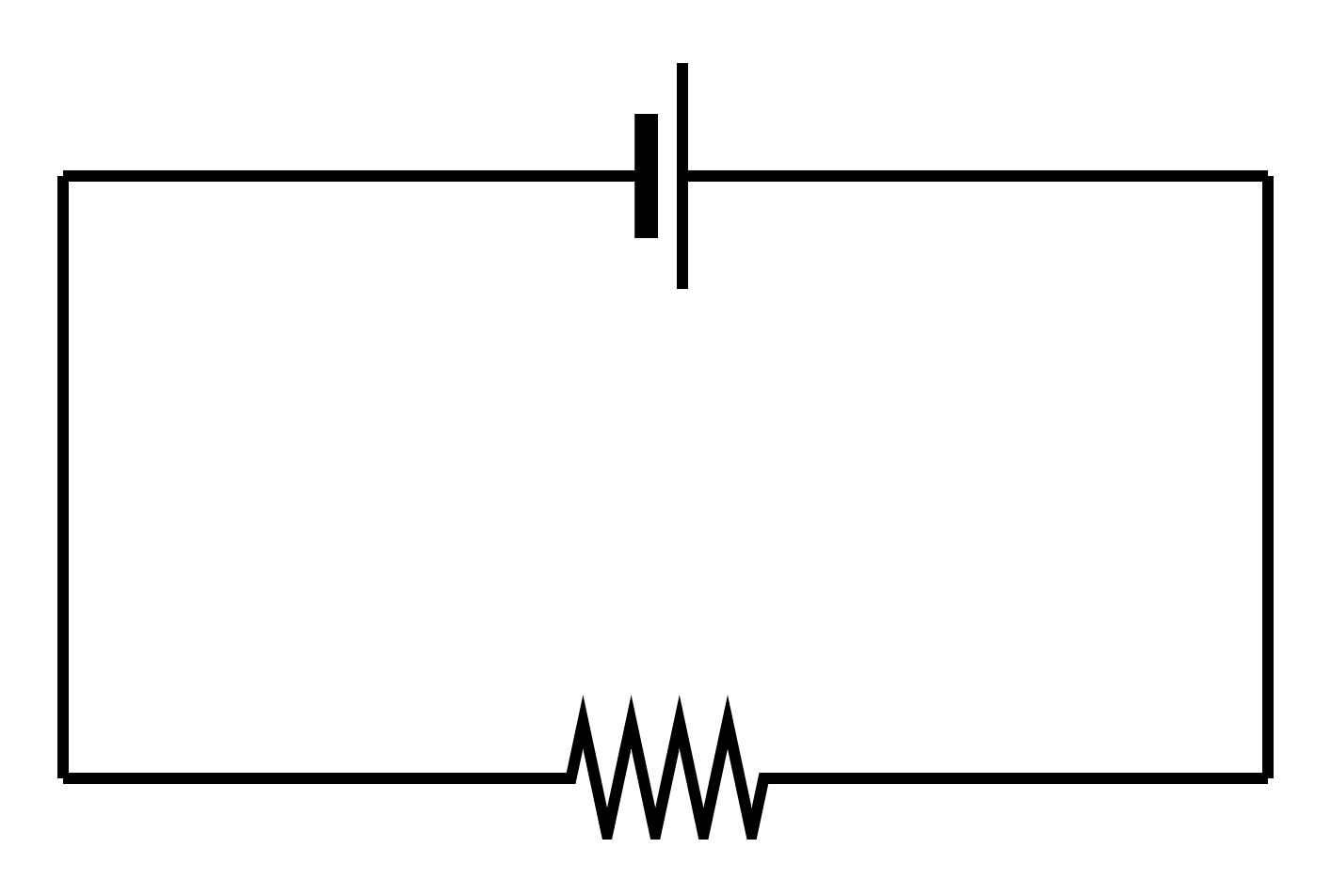
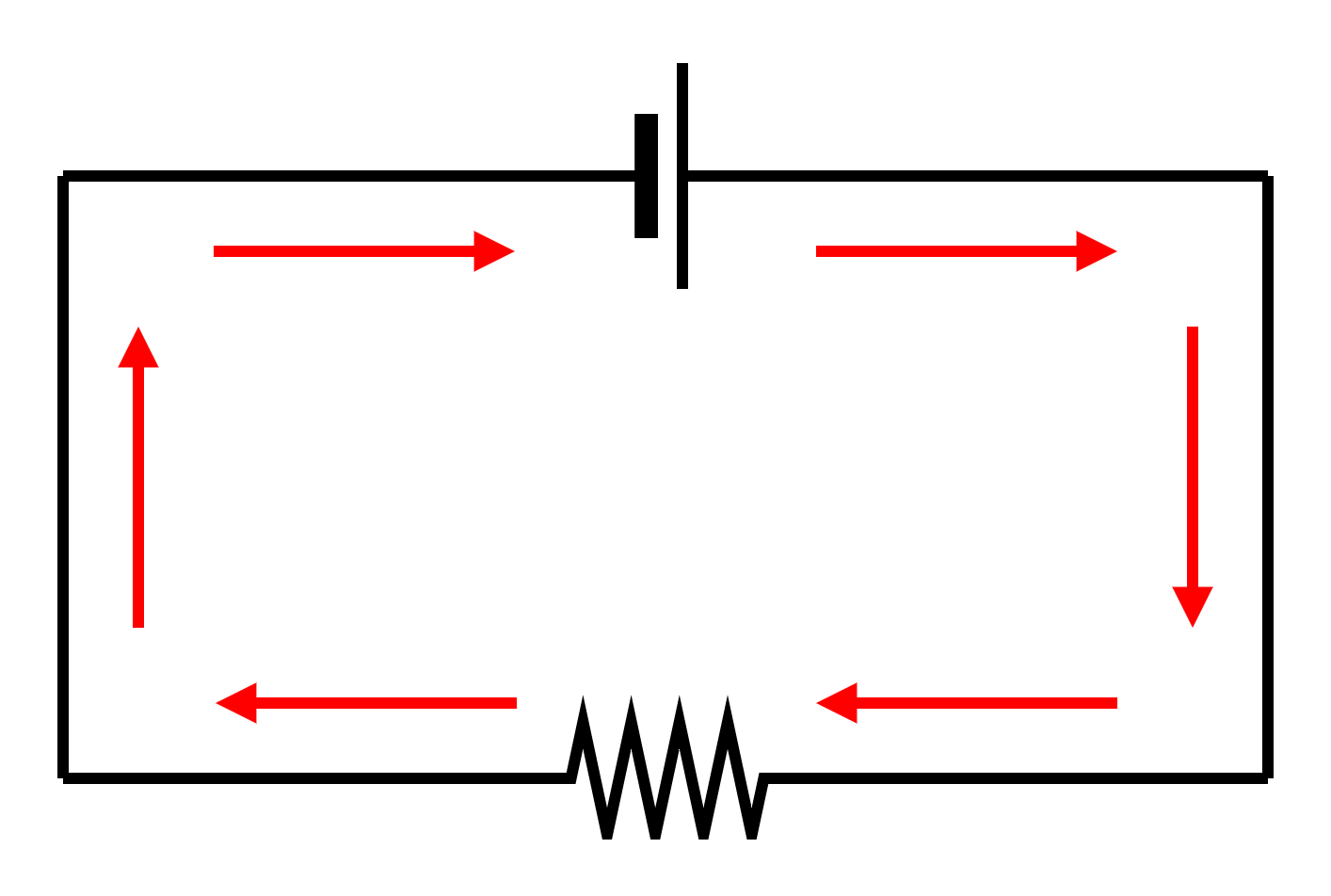
図1-1-5-4は、直流電源に抵抗器をつないだ電気回路(電子回路)です。赤い矢印は、電気の流れです。電気は、直流電源のプラス極から電気を押し出す力(電圧)によって送り出され、抵抗器で電気の流れを妨げる力(抵抗)を受け、再び直流電源のマイナス極へ戻るようすを表しています。
前述の「閉じた水路」では、「水の流れる量」に「水を押し出す力」と「水の流れを妨げる力」の二つが深く関係していました。
- 「水を押し出す力」が小さく(大きく)なる → 「水の流れる量」が少なく(多く)なる
- 「水の流れを妨げる力」が小さく(大きく)なる → 「水の流れる量」が多く(少なく)なる
電気回路(電子回路)でも、「閉じた水路」と同じ関係が成り立ちます。
- 「電気を押し出す力」が小さく(大きく)なる → 「電気の流れる量」が少なく(多く)なる
- 「電気の流れを妨げる力」が小さく(大きく)なる → 「電気の流れる量」が多く(少なく)なる
電気の世界では、この「電気の流れる量」を「電流」といい、A(アンペア)という単位で表されます。また、電子回路では、1000分の1のmA(ミリアンペア)がよく使われます。
1-1-6.電圧・電流・抵抗の関係【オームの法則】
「電圧」は「電気を押し出す力」、「電流」は「電気の流れる量」、「抵抗」は「電気の流れを妨げる力」でした。これを踏まえて、電圧・電流・抵抗の関係をみてみましょう。
- 「電圧」が小さく(大きく)なる → 「電流」が少なく(多く)なる
- 「抵抗」が小さく(大きく)なる → 「電流」が多く(少なく)なる
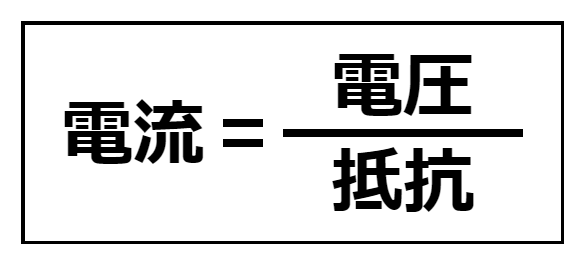
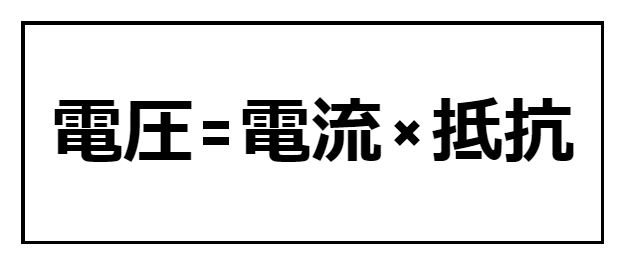
どうやら、電圧と電流には「比例」、抵抗と電流には「反比例」の関係がありそうです。実は、この関係を「オームの法則」といい、次の式で表されます。
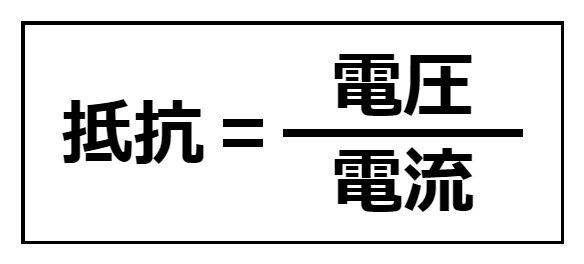
また、同式を変形すれば、以下の二式が導けます。つまり、電圧・電流・抵抗のいずれか二つが決まれば、残りの一つが計算式によって求められるということになります。
オームの法則は、基本かつ最も重要な関係式の一つです。必ず、覚えておきましょう。以下に、いくつか計算例を紹介します。
- 抵抗が10Ωの抵抗器に5Vの電圧を加えた場合、電流は0.5A(500mA)である。
- 抵抗器に12Vの電圧を加えて、電流が2Aの場合、その抵抗器の抵抗は6Ωである
- 抵抗が330Ωの抵抗器に電流が0.01A(10mA)の場合、その抵抗器に加わる電圧は3.3Vである